Infinituak, edo zenbat zenbaki zenba ditzakegun

Zenbat zenbaki daude? Galdera oso arrunta da, baina erantzunak mami handia du eta ez dago erantzun zuzen bakar bat. Infinitu erantzun genezake, baina infinitua oso termino iheskorra da eta tentu handiz ibili behar da bere inguruan. Infinitu mota ezberdinak daude, eta mota bereko infinituen artean ere erlazioak ez dira hasiera batean pentsa genitzakeenak; adibidez, eta haur baten pentsatuko lukeenaren aurka, infinitu gehi bat ez da infinitu baina zenbaki handiagoa.

Hasierako galdera nolabait zehaztuz, galde genezake: zenbaki osoak ala zenbaki bikoitiak, zeintzuk daude gehiago? Badirudi zenbaki osoak gehiago daudela. 1etik 10era adibidez, 10 zenbaki oso daude eta 5 bikoiti besterik ez. 1etik 100era 100 zenbaki oso daude eta 50 bikoiti besterik ez. Edozein zenbaki tarte hartuta ere, zenbaki osoak bikoitien kopuru bikoitzean aurki ditzakegu, eta beraz esan genezake zenbaki osoak zenbaki bikoitiak baina bi aldiz gehiago daudela.

Baina bada pentsatzeko beste modu bat ere. Zeuk zenbaki oso bat ematen badidazu, neuk berari dagokion zenbaki bikoiti bat emango dizut. Adibidez zeuk 23 zenbakia ematen badidazu, neuk 46a itzuliko dizut. Ematen didazun zenbakiaren bikoitza itzuliko dizut beti, eta edozein zenbakiri bi bidertuz zenbaki bikoitia lortzen denez, beti zenbaki bikoitia itzuliko dizut. Honela, edozein zenbaki oso berari dagokion zenbaki bikoitiarekin parekatuko dugu. Honi 1-1 erlazio edo bijekzio deritzo: bi multzo ditugu, zenbaki osoena eta bikoitiena, eta multzo bakoitzeko elementu orori beste multzoko elementu bat dagokio. Zenbaki osoen 1 elementuari zenbaki bikoitien 2 elementua dagokio. Zenbaki osoen 23 elementuari bikoitien 46 elementua. Osoen 101 elementuari bikoitien 202 elementua, eta abar, mugarik gabe. Honekin lortu duguna honako hau adieraztea da: "ez dago zenbaki osorik berari dagokion zenbaki bikoiti bat ez duenik". Eta parekatze honetan soberan geratu den zenbaki osorik ez dagoenik, ezin dugu esan zenbaki osoak zenbaki bikoitiak baina kopuru handiagoan daudenik. Hau frogatzeko infinitura jo behar izan dugu, zenbakien parekatzea mugagabea baita zenbaki handietan, baina froga baliozkoa da. Zenbaki osoen kopurua infinitu da, eta baita zenbaki bikoitiena ere, eta ezin da esan zenbaki osoak gehiago direnik.

Galdera zertxobait zaildu genezake: zenbaki osoak edo zenbaki arrazionalak, zeintzuk daude gehiago? Gogoratu zenbaki arrazionalak zatiki bidez lor daitezkeen zenbakiak direla: 2 zenbakia zenbaki arrazionala da (4/2 bezala idatzi daiteke), baita 2,5 ere, baita 2/7 edo 13/123 ere. Erantzunak argia dirudi: bi zenbaki osoren artean, nahi adina zenbaki arrazional lortu ditzakegu. 1 eta 2 zenbaki osoen artean, adibidez, 3/2, 4/3, 5/4, 6/5, ..., nahi beste zenbaki arrazional lortu ditzakegu; infinitu zenbaki arrazional daude edozein bi zenbaki osoren tartean. Beraz, bi zenbaki oso bakoitzeko infinitu zenbaki arrazional badaude, badirudi denak zenbatuko bagenitu zenbaki arrazionalak zenbaki osoak baino gehiago leudekela.

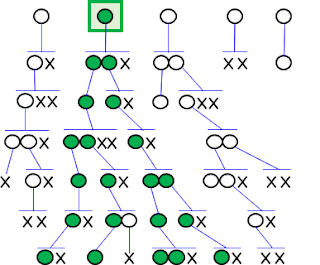
Saiatu gintezke zenbaki osoen eta arrazionalen artean bijekzio bat sortzen. Lortuko bagenu, bien kopurua berbera dela frogatuko genuke! Beheko irudian ikus daiteke hau nola lortu daitekeen. Zenbakitzaile berbera duten zatikiak lerro batean jartzen dira, izendatzaileak txikienetik handienera ordenatuz. Zenbakitzaile ezberdina dutenak ilara ezberdinetan jartzen dira. Hala, lauki bat osatzen da zutabe eta lerro kopuru infinituaz, non zutabe bakoitzean izendatzaile denak berberak izango diren, eta ilara bakoitzean zenbakitzaileak berberak izango diren. Zalantzarik ez dago lauki honetan zatiki posible guztiak daudela, eta beraz zenbaki arrazional guztiak. Zatiki asko zenbaki bera izango dira (adibidez 1/2 edo 2/4), baina honek ez digu axola. Orain, zenbaki guzti hauek zenbatzea lortu behar dugu. Ezkerretik eskuinera normal zenbatu beharrean, diagonalean zenbatuko ditugu, irudian agertzen den bezala. Zenbatzeko modu hau muga gabe jarraituz, laukiko zatiki guztiak zenbatu ahal izango ditugu. Argi dago infinitu zatiki zenbatuko ditugula, baina arazoaren koska zenbatzeko gai izango garela da. Zenbatzeko gai bagara, zatiki bakoitzari zenbaki oso bat parekatzeko gai izango gara. Hau da, lehen zatikia 1 zenbakiarekin parekatuko dugu, bigarren zatikia 2 zenbakiarekin, hamargarren zatikia 10 zenbakiaren, eta abar. Modu honetan, edozein zatiki zenbaki oso ezberdin batekin parekatuta geratuko da. Alderantzizkoa ere lortua izango dugu: edozein zenbaki osori zenbaki arrazional bat baitagokio, 100 zenbakiari adibidez zatikiak zenbatzeko erabili dugun bidean ehungarren zatikia dagokio. Beraz, zenbaki arrazional bakoitzari zenbaki oso bat dagokionez, eta alderantziz, bi multzoen arteko bijekzio edo 1-1 erlazio bat dugu, eta berriro baieztatu ahal izango dugu zenbaki osoen kopurua eta zenbaki arrazionalena berbera dela.

Azken adibidearekin lortu duguna zenbaki arrazionalak zenbatzea da. Orokorrean esan dezakegu zenbaki multzo bat zenbatzeko modurik badugu, eta zenbaki kopurua infinitua bada, orduan zenbaki multzo horren kopurua zenbaki osoen kopuruaren berbera dela. Infinitu da kasu guztietan, baina infinitu mota berbera. Multzo hauei multzo zenbakigarri deritzaie, bere elementuak zenbatu daitezkeelako.

Esan bezala, multzo zenbakigarri infinitu guztien elementu kopurua berbera da. Infinitu da kopuru hau, baina infinitu mota zehatz bat. Multzo baten elementu kopurua multzoaren kardinalitatea da, eta kardinalitate ezberdinak bereizteko zenbaki bereziak erabiltzen dituzte matematikariek. Aleph zenbakiak dira, $ \aleph $ sinboloaz idazten direnak, eta multzo zenbakigarri infinituen kardinalitatea aleph-zero edo $ \aleph_0 $ bezala definitzen da. Beraz, esan dezakegu zenbaki oso, zenbaki bikoiti, eta zenbaki arrazionalen kopurua, denena, $ \aleph_0 $ dela.

Baina hau al da zenbaki guztien kopurua? Zenbaki irrazionalak (zatiki bezala adierazi ezin daitezkeenak, erro 2 edo $ \pi $ bezalakoak) kanpoan uzten ari gara, eta begiratu beharko genuke ea zenbaki errealen multzoa zenbakigarria den ala ez. Georg Cantor matematikariak 1871an frogatu zuen ez zegoela 1-1 erlaziorik edo bijekziorik zenbaki errealen eta zenbaki osoen artean. Saiatu bat aurkitzen, gorago zenbaki arrazionalek egin dugun bezala! Ezinezkoa da! Zenbaki errealen multzoa, beraz, ez-zenbakigarria da, eta bere kardinalitatea (kontinuoaren kardinalitatea bezala ezagutua eta $ \mathfrak{c} $ sinboloaz adierazten dena) zenbaki osoena $ \aleph_0 $ baino handiagoa da. Bide batez, zenbaki irudikarien kardinalitatea ere $ \mathfrak{c} $ da. Cantor berak frogatu zuen, gainera, $ \aleph_0 < \mathfrak{c} = 2^{\aleph_0} $ betetzen dela. Oraindik ere, matematiketako erantzunik gabeko galdera garrantzitsuenetako bat da egiaztatzea ea $ \mathfrak{c} = \aleph_1 $ betetzen den, zeinak esan nahi duen ez dagoela multzorik zenbaki osoena baino kardinalitate handiagoa eta zenbaki errealena baino txikiagoa duena.

Beraz, zenbat zenbaki dauden galderari, erantzuna zenbaki hitzaz zer esan nahi dugunaren araberakoa da. Zenbaki osoez ari bagara (edo arruntez, edo arrazionalez), orduan erantzuna infinitu zenbakigarria edo $ \aleph_0 $ izango litzateke. Zenbaki errealez ari bagara, kontinuoaren kardinalitatea edo $ \mathfrak{c} $ izango litzateke. Infinitu mota ezberdinetan dago erantzuna, beti ere!