Mezuak

Eba mitokondriala: gizaki guztion amona

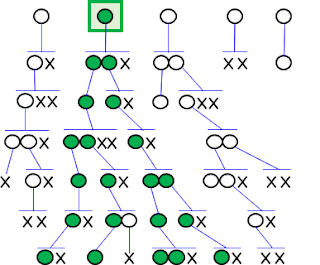
Irudia
Gizaki guztiok, gure zuhaitz genealogikoa amen adarretatik jarraituz, emakumezko arbaso berbera dugu, denon birramona deitu ahal geniokeena. Azken ikerketen arabera, Eba mitokondriala deituriko hau duela 155.000 urte inguru bizi izan zen, Afrikan seguru aski. Eba mitokondriala gaur egungo gizaki guztien arbasoa da, zuhaitz genealogikoa emakumeen adarretatik bakarrik jarraituz. Zuhaitza atzeraka jarraituz, amaren amaren, bere amaren, eta abarren arrastoari segiz, iritsiko da belaunaldi bat non gizaki guztiok emakume berera iritsiko garen: gu denon birramona, Eba mitokondriala. Honek ez du esan nahi Eba mitokondriala garai hartako emakume bakarra zenik; beste milaka emakume egongo ziren eta euren seme-alabak izango zituzten, baina beste haietako inoren oinordekoak ez dira gaur arte alabaz alaba iritsi, tartean gizonezko oinordekorik izan gabe. Ez du esan nahi ere bakoitzaren arbaso emakumezko bakarra denik; bi amona eta lau birramona ditugun bezala, duela 155.000 urteri dagokion bela
Argitaratu iruzkina
Gehiago ikusi »

Zizarezuloaren afera: zer gertatu da

Irudia
"Zizare-zulo bat sortu dute ordenagailu kuantiko bat erabiliz." Izenburu hori zuen albisteak bere berri eman zuen Quanta aldizkarian. Fisika teorikoaren zutarriak dardarka jarri zitzakeen halako izenburudun ikerketa batek, baina behin dardarizoa pasata, guztia ezerezean geratu da. Sekulako oihartzuna izan bazuen ere, fisikariak ados jartzen ari dira esperimentu arrunt bat gehiago besterik ez zela izan esatean. Zer gertatu zen, zergatik horrelako oihartzuna? Duela bi aste Nature aldizkarian argitaratu zuten: Googlen ordenagailu kuantiko batean zizare-zulo bat sortu zuten. Gure txio harian azaltzen saiatu ginen zer argitaratu zen. Motzean esanda, korapilatze kuantikoa erabiliz sistema kuantiko konkretu bat sortu zuten, eta AdS/CFT delako korrespondentziaren arabera, sistema kuantiko hori matematikoki zizare-zulo sinplifikatu baten parekidea da. Berriak sekulako oihartzuna izan zuen. Quanta aldizkari zientifikoa izan zen xehetasun gehien eman zituena, albistearen inguruko pri
Argitaratu iruzkina
Gehiago ikusi »

Inflazioa: Big Bangaren lehen uneak

Irudia
Ezaguna zaigu Big Bangaren teoria eta ondo errotuta dago fisikarien artean, baina unibertsoak baditu ezaugarri batzuk Big Bangak soilik azaldu ezin dituenak. Inflazioaren eredua Big Bangaren lehen uneetan kokatzen da, eta ezaugarri hauetako batzu azaltzeko gai da. Unibertsoaren jatorria azaltzen duen Big Bang teoria nahikoa ondo zehaztuta badago ere, zalantza asko daude bere lehen uneen inguruan. Teoriak dio gure unibertsoa duela gutxi gora behera 14 mila milioi urte zegoen singularitate batetik sortu zela, eta unibertsoa etengabe hedatzen egon dela gaur arte. Big bang teoriaren onarpen orokortua 1964an etorri zen, CMBa delakoaren aurkikuntzarekin. CMB edo Hondoko Mikrouhin-Erradiazioa ( Cosmic Microwave Radiation ingelesez) Lurretik antzeman dezakegun erradiazio elektromagnetikoa da, unibertsoaren mutur-muturretik datorkiguna. Kosmosean urruneko objetuak ikusten ditugunean, orduan eta urrunago begiratu orduan eta gauza zaharragoak ikusten ditugu, argiaren abiadura finitua dela et
Argitaratu iruzkina
Gehiago ikusi »