Game of Life: Bizitzaren Jokoa
Arau gutxi eta errazeko joko honek erakusten du nola hasierako baldintza ezberdinetatik abiatuta posible den sistema batek bilakaera oso ezberdin eta konplexuak izatea. Bizitza bera ere (jaiotza, heriotza, ugalketa) simulatzeko gai da.
Arauak
Laukiz osaturiko taula batean jokatzen da. Lauki bakoitza bizirik ala hilik egon daiteke, eta hurrengo belaunaldian nola egongo den bere bizilagunek (bertikalean, horizontalean eta diagonalean) zehazten dute:
Bizirik den lauki batek bizirik dauden 2 edo 3 bizilagun baditu bizirik jarraitzen du.
Bizirik den lauki batek bizirik dauden 2 bizilagun baino gutxiago baditu hil egiten da, biztanleria faltagatik.
Bizirik den lauki batek bizirik dauden 3 bizilagun baino gehiago baditu hil egiten da, gain-populazioagatik.
Hilik dagoen lauki batek bizirik dauden 3 bizilagun baditu bizirik egotera pasatzen da, ugalketaz.
Jokalariak taularen lehen egoera bakarrik zehazten du, bizirik zein lauki dauden aukeratuz. Hortik aurrera, sistemak bilakaera autonomoa du aurreko arauek definitzen dutenaren arabera.
Adibidea
Adibide bat ikus dezagun. Demagun lauki horiak bizirik dauden laukiak direla, eta lauki grisak hilik dauden laukiak. Hasierako egoera honako hau izan daiteke:
Kasu honetan lauki hori guztiek 2 edo 3 bizilagun dituzte, beraz bizirik mantenduko dira. Gainera, goiko puntaren bi aldeetako lauki grisek, eta baita formaren azpian erdiko lauki grisak ere, 3 bizilagun hori dituzte, beraz hurrengo pausoan hori izatera (bizirik egotera) pasako dira. Horrela, hurrengo belaunaldian honako egitura izango dugu:
Oraingo honetan lauki hori askok bizilagun gehiegi dituzte, beraz gain-populazioa dela eta hil egingo dira. Bizirik geratuko direnak goiko lerroko bi iskinak, eta azpialdeko erpina dira. Baina beste batzuk jaioko dira: goiko lerroaren gaineko erdiko laukia eta azpialdeko erpinaren bi aldeetakoak:Hurrengo belaunaldian, erdiko zutabean ez dauden eta bizirik dauden lauki guztiak hilko dira, bizilagun bakarra bait dute. Dena den, beste lauki batzuk jaioko dira, honako irudia lortuz:
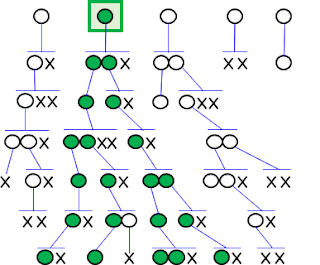
Gisa berean jarraituta sistemak bilakaera luzea izango du. Sistema hau ez da inoiz hiltzen (ez dira lauki guztiak une berean hilda geratzen), eta bi egoera artean txandakatuz amaitzen da bere bilakaera. Ondorengo irudian ikus daiteke bere bilakaera osoa, lehenengo belaunalditik abiatuta:Sistema konplexuagoak
Aurreko hau inoiz amaitzen edo hiltzen ez den joko baten adibidea da. Hasiera egoera askok belaunaldi gutxiren buruan lauki guztik hilik egotera eramaten dituzte. Beste batzuek egitura finkoak sortzera eramaten dute; 2x2 lauki bat, adibidez, egitura finkoa da eta aldaketarik gabe bizirik dirau belaunaldiz belaunaldi.
Badaude egitura bereziagoak ere. Espaziontzi deritzaien egiturak beraien hasierako formara itzultzen dira belaunaldi batzuren buruan, baina taulako beste kokapen batetan. Horrela, taulan barrena barreiatzen dira. Espaziontzi arruntena planeagailu edo glider delakoa da; une bakoitzean bizirik dauden 5 lauki besterik ez ditu. Hona hemen planeagailu baten bilakaera:
Baina hau hasiera besterik ez da. Bizitzaren Jokoaren inguruan komunitate handia dago, egitura edo sistema berritzaileak bilatzen dituena, zein baino zein interesgarriagoak. Badaude pistola deituriko egiturak, zeintzuk espaziontziak etengabe sortzeko gai diren. Beheko honek planeagailuak sortzen ditu, eta taularen alde baterantz jaurti:
Propietate emergenteak
Bizitzaren Jokoa John Conway matematikariak asmatu zuen 1970an. Aurretik baziren antzeko beste modelo batzuk, modu orokorrean Automata Zelularrak deituak. Haiek ere laukien balio ezberdinetan eta bizilagunen egoeretan oinarritzen ziren, baina arau ezberdinak zituzten. Dena den, Bizitzaren Jokoa izan zen automata hauek publiko orokorrera zabaldu zituena eta modeloa joko bezela aurkeztu zuena. Halako jokoei zero jokalariko jokoak deritzaie, behin hasierako baldintzak ipinita, giza jokalaririk ez bait da behar jokoak aurrera egiteko.
Ikusi dugunaren arabera, Bizitzaren Jokoak propietate emergenteak ditu. Arau oso arrunt batzutatik abiatuta, lauki txikiei eragiten diena, sistema oso konplexuak lortu daitezke, hasiera baldintzak jakinda ia aurrikusi ezin direnak. Hau dela eta ikerketa asko egin dira jokoaren inguruan, bai matematikarien aldetik, bai informatikarien aldetik, eta baita filosoen aldetik ere.
Alde batetik, jokoa Turing osoa dela egiaztatu zen. Honek esan nahi du alde batetik jokoa ordenagailu baten modura erabil daitekeela: sarrera datuak eman, kalkuluak egiten utzi, eta irteera jaso. Eta, bestetik, ordenagailu konbentzional batek egin ditzakeen kalkulu guztiak egiteko gai dela. Ezin zaizkio datuak teklatu batetatik komandoz sartu, baina bere hizkuntzan emanez gero (lauki hilak eta biziak), kalkulu berberak egiteko gai da.
Filosofia aldetik ere zeresan handia du jokoak, batez ere 2010ean bere burua erreplikatzeko gai zen egitura bat aurkitu zutenean. Egiturak bere burua bezalako berri bat sortzen du bere ondoan, eta ondoren egitura sortu berriak jatorrizko egitura zaharra deusezten du. Ugalketa asexualaren antz handia du sistema honek. Hemen bideo bat sistema hau deskribatzen duena:
Aurretik ere Automata Zelularretan ezagunak ziren euren burua erreplikatzen zuten sistemak. John von Neumann matematikari handiak 1940an diseinatu zuen bere "eraikitzaile unibertsala", lehen halako sistema. Egitura honek ere bere burua erreplikatzen du; eraikitako egitura berriak, era berean, bere burua erreplikatzen du, eta horrela etengabe. Sistema honek gainera mutazioak ere jasan ditzake: egituretako bat eskuz manipulatzen bada bere itxura aldatuz, aldaketa hori hurrengo belaunaldietako egituretara ere pasatzen da.
Hain arau arruntetatik abiatuta halako sistema konplexuak egoteak, ugalketarako gai direnak, bizitzaren esanahiaren inguruan zer pentsatua ematen du. Izaki bizidunen egiturekin antz handia dutela esan daiteke. Biologia osoa kimikako arauetan oinarritzen da, eta kimika berriz fisikako arauetan, eta badirudi fisikako arauak oinarri-oinarrian gutxi eta arruntak izan daitezkeela (fisika teorikoko ikertzaileak hauen bila ari dira). Automata Zelular hauek bizitza artifizialaren adibide direla esaten da, eta zailtasunak ipintzen dituzte bizitza bera zer den definitzeko garaian.









Iruzkinak
Argitaratu iruzkina
Sartu hemen zure iruzkina